Empirical Orthogonal Functions
Empirical orthogonal functions (EOFs; Lorenz (1956)) provide a handy framework for multivariate data analysis. Here EOFs refer to a class of data objects, however, in a more general context, EOFs refer to the spatial coherent structures which maximise the variance, whereas the principal components (PCs) refer to time series describing the degree of their presence at any time. The eigenvalues refer to the variance of each EOF mode. In ‘esd’, the EOFs are estimated using a singular value decomposition (SVD) (Press et al., 1989a; Strang, 1988):
//( X = U \Lambda V^T )//, (2)
where \( X\) is a matrix of data with two dimensions (space, time),\(U\) hold the EOF patterns, \(Λ\) is a diagonal matrix with the eigenvalues, and \(V\) contains the PCs. The EOFs are used to extract the essence of the information embedded in the data, taking advantage of redundancy and emphasising the most prominent characteristics. Example 4.1 shows how the EOFs can be estimated and visualised in ‘esd’.
The EOFs are used as input to other analysis, such as downscaling (DS) and canonical correlation analysis (CCA). It is also possible to recover the original data from EOFs through eof2field, however, the number of EOFs are usually truncated, and only the most prominent features are recovered. The function eof2field can be used to filter the data in terms of removing small scale and noisy features.
The EOFs can provide an indication of some of the most prominent phenomena in the climate system, such as the annual cycle, the El Ni˜no Southern Oscillation, and the Arctic Oscillation.
Principal Component Analysis
The method called PCA - principal component analysis - is similar to EOF, but is designed for groups of stations rather than gridded fields (Example 4.2). The PCA can also be used to represent data on an irregular grid (such as rotated fields from regional climate models). It is possible to grid the spatial modes of the PCA onto a regular grid, and hence convert the pca class into a eof class (the gridding is currently not performed in esd, but could be done using optimal interpolation, or kriging taking geographical features into account (Benestad et al., 2012)). Whereas EOF weights each grid box with its grid box area, PCA does not apply any weighting to the different series (which may imply that correlated variability from nearby stations is emphasised by the PCA).
PCAs are useful for investigating large-scale dependency, as the leading mode will pick up patterns with coherent variations across the stations. They are also used in CCA and identifying stations with suspect data.
Canonical Correlation Analysis
Canonical correlation analysis (CCA) can be used to explore dependencies between different data sets (Example 4.3). It is a useful tool for investigating suitable predictors for downscaling or identifying tele-connections. Sometimes it can provide some indications of suspect station data. The computation of the CCA in ‘esd’ is based on the method by Barnett-Preisendorfer (Barnett and Preisendorfer , 1987; Wilks, 1995). The inputs are either an ‘pca’ or ‘eof’ class.
Other types of analysis
Methods such as singular spectrum analysis (SSA) and ‘coherence’ have been adapted from the ‘clim.pact’ package, but have not been elaborated and tested yet for the ‘esd’ objects. There is also a set of low-pass filters such as filt. Other type of analysis can be included such as performing a multivariate regression analysis (MVR) and using eof to do the downscaling.
Predict & project
In ‘esd’, the S3 method ‘predict’ is extended to the ‘ds’ class and may be extended to CCA (cca) and singular spectrum analysis (ssa) in the future. The call predict will return the downscaled results for the calibration method by default, but can also be used to return a projection if the downscaling was based on a common EOF or a prediction based on a new EOF. The method ‘project’ is a more specific version of ‘predict’ that returns results from a projection (Example 4.4). The downscaled results from a projection are also contained in the ds object.
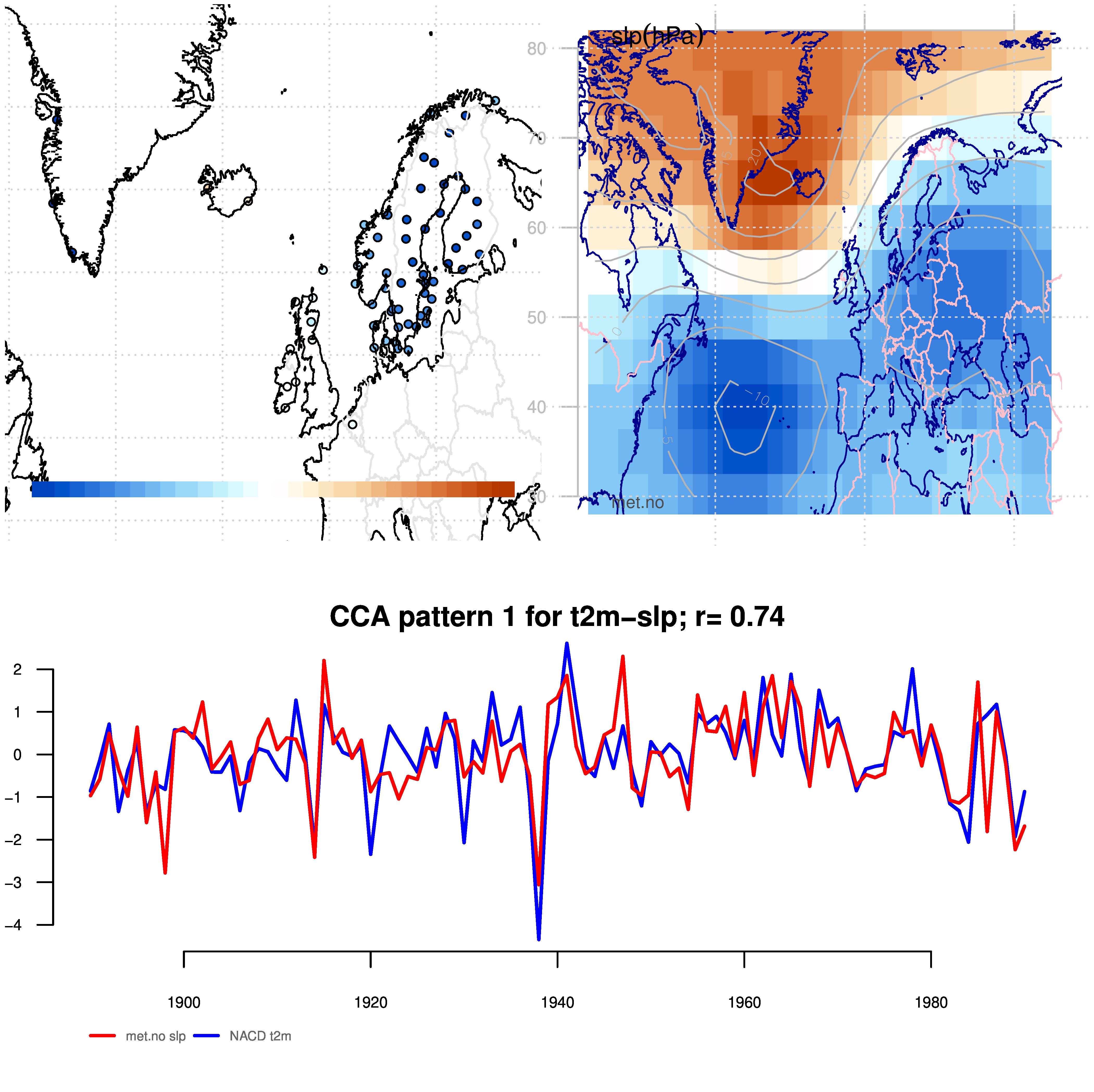Figure 18: Plot of CCA analysis based on PCs of annual mean surface temperature and EOF of annual mean Sea level pressure from DNMI.
Trajectory objects
The esd package includes functions for statistical analysis and visualisation of trajectory data, e.g., the paths of extra-tropical cyclones or ice bergs. Many of the standard tools and methods are applicable to ‘trajectory’ objects, e. g., limiting the range of data by subset, visualising the trajectories by map or plot, as well as principal component analysis and downscaling (PCA and DS).
The trajectory methods have been designed with the analysis of storm tracks in mind, in particular cyclone path data produced under the IMILAST (Inter-comparison of mid latitude storm diagnostics) project (Neu et al., 2012). Trajectory data that follow the format specified for IMILAST can be imported into R using the function ‘read.imilast’. The IMILAST data must then be transformed into a trajectory object with the function ‘trajectory’ before other esd methods can be applied.
x <- read.imilast(filename,path=pathtofile)
y <- trajectory(x)
The function ‘trajectory’ transforms a data frame containing spatio-temporal information about trajectories of variable length to a matrix with the trajectories interpolated to the same length (by default 10). The input to ‘trajectory’ must for every time step include a ‘Trajectory’ id number, as well as geographical (latitude, longitude) and temporal (year, month, day, and time) information, and optionally a quality flag (Code99). Other parameters describing the evolution of the trajectory may also be included and will then be interpolated and passed on to the ‘trajectory’ object. Meta data can be entered as arguments to the ‘trajectory’ function, e.g. a description of the parameter (‘param’ or ‘longname’), the source of the data (src), or references to a paper, website or method (reference, URL, method). A sample file, imilast.M03, containing trajectories of deep cyclones in the North Atlantic region comes with esd and is provided in its examples. These storm paths were obtained by cyclone identification in a gridded data set (ERAinterim, 1.5◦ resolution) using a calculus based
cyclone identification (CCI) algorithm (Benestad and Chen) (method 3 of IMILAST). In the future, ‘esd’ will be extended to cyclone identification and tracking using this CCI method.
Example 4.5 demonstrates how to select a subset of trajectories and plot the annual storm count using the function plot.trajectory(). The spatial extent of the trajectories can be plotted either as individual tracks on a map by the function map.trajectory(), or as the number density (unit: year−1 1000km−2) by map.density.trajectory (Example 4.6). Principal component analysis of trajectory objects is by default applied to the longitude and latitude displacement with regards to the starting point of the individual trajectories (Example 4.7).
Figure 19: The annual storm count for all months (black) is plotted using ‘plot.trajectory’. A storm count for the winter season (DJF, blue) is then obtained by ‘count.trajectory’ and added to the figure.
Figure 20: Maps of storm trajectories in the North Atlantic region created with ‘map.trajectory’ (left) and ‘map.density.trajectory’ (right).
Figure 21: Plot of the first (red) and second (blue) principal component obtained by PCA of storm tracks in the North Atlantic region (a). In the map (b), the solid and dashed lines represent the maximum extent of the component in the positive and negative direction, respectively. The pca figures are produced with the functions ‘plot.pca.trajectory’ (a) and ‘map.pca.trajectory’ (b).